DL notes 02: ML/DL模型训练的Tips
@[toc]
一、基本概念
训练误差(training error):指模型在训练数据集(train dataset)上表现出的误差。
泛化误差(generalization error):指模型在任意一个测试数据样本上表现出的误差的期望,并常常通过测试数据集(test dataset)上的误差来近似。
损失函数(loss function):计算训练误差和泛化误差可以使用之前介绍过的损失函数,例如线性回归(linear regression)用到的平方损失(squared loss)函数和softmax回归用到的交叉熵(cross entropy)损失函数。
训练数据集(train dataset):【模型】(Model)训练的过程其实就是在求【参数】的过程,我们先假定某类【模型】(比如决策树模型),然后用【训练集】来训练,学习到对应的最优的【参数】。但是问题在于,我们没有办法保证我们假设的那个【模型】是最优的,我们极有可能假设错误对吧。那怎么办呢?有一个简单的解决方案就是我们假设一堆的模型,然后用【训练集】分别对这些模型来进行训练,学习到每一个【模型】中分别对应的参数。这是训练模型的第一步,也就是【训练集】的任务。(*以上摘录自答疑汇总*)影响欠拟合和过拟合的另一个重要因素是训练数据集的大小。一般来说,如果训练数据集中样本数过少,特别是比【模型参数】数量(按元素计)更少时,过拟合(overfitting)更容易发生。此外,泛化误差不会随训练数据集里样本数量增加而增大。因此,在计算资源允许的范围之内,我们通常希望训练数据集大一些,特别是在模型复杂度较高时,例如层数较多的深度学习模型。
验证数据集(validation dataset):从严格意义上讲,测试数据集只能在所有超参数和模型参数选定后使用一次。不可以使用测试数据选择模型,如调参。由于无法从训练误差估计泛化误差,因此也不应只依赖训练数据选择模型。鉴于此,我们可以预留一部分在训练数据集和测试数据集以外的数据来进行模型选择。这部分数据被称为验证数据集,简称验证集(validation set)。例如,我们可以从给定的训练集中随机选取一小部分作为验证集,而将剩余部分作为真正的训练集。
测试数据集(test dataset):当通过损失函数和评价指标(evaluation metric)判断学习到【参数】和【超参数】后,就确定具体模型和模型的参数,需要新数据来测试模型效果。因此,不能使用之前的数据,而单独构建全新数据集,即【测试集】。这个时候我们就要来看最后的结果怎么样,如果结果很好,那么说明一切顺利,但是如果结果很差,那问题出在哪里呢?其中可能的一个原因就是我们事先假定的那一类的【模型】(比如我们最先选择的决策树模型)并不是适合来分析这些数据,因此哪怕我们选择出了这一堆决策树模型中最好的一个(超参数的选择过程),它的效果依旧不怎么样。(*摘录自答疑汇总*)
k-fold 交叉验证:由于验证数据集不参与模型训练,当训练数据不够用时,预留大量的验证数据显得太奢侈。一种改善的方法是K折交叉验证(K-fold cross-validation)。在K折交叉验证中,我们把原始训练数据集分割成K个不重合的子数据集,然后我们做K次模型训练和验证。每一次,我们使用一个子数据集验证模型,并使用其他K-1个子数据集来训练模型。在这K次训练和验证中,每次用来验证模型的子数据集都不同。最后,我们对这K次训练误差和验证误差分别求平均。
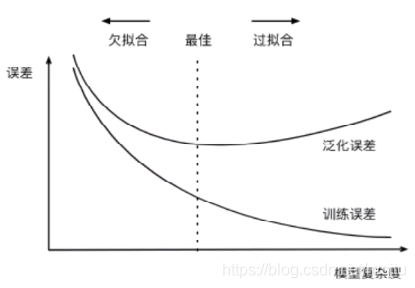
欠拟合(underfitting):模型无法得到较低的训练误差,我们将这一现象称作欠拟合(underfitting)。
过拟合(overfitting):模型的训练误差远小于它在测试数据集上的误差,我们称该现象为过拟合(overfitting)。
模型复杂度:为了解释模型复杂度,我们以多项式函数拟合为例。给定一个由标量数据特征$x$和对应的标量标签$y$组成的训练数据集,多项式函数拟合的目标是找一个$K$阶多项式函数
$$ \hat{y} = b + \sum_{k=1}^K x^k w_k $$ 来近似 $y$。在上式中,$w_k$是模型的权重参数,$b$是偏差参数。与线性回归相同,多项式函数拟合也使用平方损失函数。特别地,一阶多项式函数拟合又叫线性函数拟合。
给定训练数据集,模型复杂度和误差之间的关系:
二、应对欠拟合和过拟合的解决方法
2.1 欠拟合的解决办法
这里仅以个人经验列举一些普通操作: 1.提升现有模型的复杂度,提升模型的描述能力 2.更换合适的模型 3.检查损失函数是否适合模型优化过程
2.2 过拟合的解决办法
2.2.1 权重衰减 / $L_{2}$范数正则化
权重衰减等价于 $L_2$ 范数正则化(regularization)。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小,是应对过拟合的常用手段。$L_2$范数正则化在模型原损失函数基础上添加$L_2$范数惩罚项,从而得到训练所需要最小化的函数。$L_2$范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。以线性回归中的线性回归损失函数为例
$$ \ell(w_1, w2, b) = \frac{1}{n} \sum{i=1}^n \frac{1}{2}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right)^2 $$ 其中$w_1, w_2$是权重参数,$b$是偏差参数,样本$i$的输入为$x_1^{(i)}, x_2^{(i)}$,标签为$y^{(i)}$,样本数为$n$。将权重参数用向量$\boldsymbol{w} = [w_1, w_2]$表示,带有$L_2$范数惩罚项的新损失函数为
$$ \ell(w_1, w_2, b) + \frac{\lambda}{2n} |\boldsymbol{w}|^2, $$ 其中超参数$\lambda > 0$。当权重参数均为0时,惩罚项最小。当$\lambda$较大时,惩罚项在损失函数中的比重较大,这通常会使学到的权重参数的元素较接近0。当$\lambda$设为0时,惩罚项完全不起作用。上式中$L_2$范数平方$|\boldsymbol{w}|^2$展开后得到$w_1^2 + w_2^2$。 有了$L_2$范数惩罚项后,在小批量随机梯度下降中,我们将线性回归一节中权重$w_1$和$w_2$的迭代方式更改为
$$ \begin{aligned} w_1 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w1 - \frac{\eta}{|\mathcal{B}|} \sum{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\ w_2 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w2 - \frac{\eta}{|\mathcal{B}|} \sum{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right). \end{aligned} $$
其中$|\mathcal{B}|$为小批量的样本数,$\eta$代表每一个小批量数据对应梯度下降的步长参数,类似SGD中的$\alpha$(为保证严谨,这里不使用学习率来表达),pytorch的torch.optim.SGD也直接封装了权重衰减的参数。可见,$L_2$范数正则化令权重$w_1$和$w_2$先自乘小于1的数,再减去不含惩罚项的梯度。因此,$L_2$范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制,这可能对过拟合有效。
2.2.2 dropout
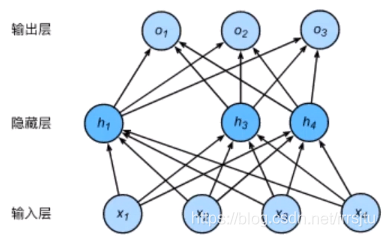
多层感知机中神经网络图描述了一个单隐藏层的多层感知机。其中输入个数为4,隐藏单元个数为5,且隐藏单元$h_i$($i=1, \ldots, 5$)的计算表达式为
$$ h_i = \phi\left(x1 w{1i} + x2 w{2i} + x3 w{3i} + x4 w{4i} + b_i\right) $$ 这里$\phi$是激活函数,$x_1, \ldots, x4$是输入,隐藏单元$i$的权重参数为$w{1i}, \ldots, w_{4i}$,偏差参数为$b_i$。当对该隐藏层使用丢弃法时,该层的隐藏单元将有一定概率被丢弃掉。设丢弃概率为$p$,那么有$p$的概率$h_i$会被清零,有$1-p$的概率$h_i$会除以$1-p$做拉伸。丢弃概率是丢弃法的超参数。具体来说,设随机变量$\xi_i$为0和1的概率分别为$p$和$1-p$。使用丢弃法时我们计算新的隐藏单元$h_i’$
$$ h_i’ = \frac{\xi_i}{1-p} h_i $$ 由于$E(\xi_i) = 1-p$,因此
$$ E(h_i’) = \frac{E(\xi_i)}{1-p}h_i = h_i $$
即丢弃法不改变其输入的期望值。让我们对之前多层感知机的神经网络中的隐藏层使用丢弃法,一种可能的结果如图所示,其中$h_2$和$h_5$被清零。这时输出值的计算不再依赖$h_2$和$h_5$,在反向传播时,与这两个隐藏单元相关的权重的梯度均为0。由于在训练中隐藏层神经元的丢弃是随机的,即$h_1, \ldots, h_5$都有可能被清零,输出层的计算无法过度依赖$h_1, \ldots, h_5$中的任一个,从而在训练模型时起到正则化的作用,并可以用来应对过拟合。在测试模型时,我们为了拿到更加确定性的结果,一般不使用丢弃法。
三、梯度消失和梯度爆炸
深度模型有关数值稳定性的典型问题是消失(vanishing)和爆炸(explosion)。当神经网络的层数较多时,模型的数值稳定性容易变差。
假设一个层数为$L$ 的多层感知机的第 $l$ 层 $H^{(l)}$ 的权重参数为 $W^{(l)}$ ,输出层 $H^{(L)}$ 的权重参数为 $W^{(L)}$ 。为了便于讨论,不考虑偏差参数,且设所有隐藏层的激活函数为恒等映射(identity mapping)$\phi(x)=x$ 。给定输入 $X$ ,多层感知机的第 $l$ 层的输出 $H(l)=XW(1)W(2)…W(l)$ 。此时,如果层数 $l$ 较大, $H^{(l)}$ 的计算可能会出现衰减或爆炸。举个例子,假设输入和所有层的权重参数都是标量,如权重参数为$0.2$和$5$,多层感知机的第30层输出为输入 $X$ 分别与 $0.2^{30}≈1×10^{−21}$ (消失)和 $5^{30}≈9×10^{20}$(爆炸)的乘积。当层数较多时,梯度的计算也容易出现消失或爆炸。
四、随机初始化模型参数
在神经网络中,通常需要随机初始化模型参数。回顾多层感知机一节描述的多层感知机。为了方便解释,假设输出层只保留一个输出单元 $O{1}$ (删去 $O{2}$ 和 $O_{3}$以及指向它们的箭头),且隐藏层使用相同的激活函数。如果将每个隐藏单元的参数都初始化为相等的值,那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值,并传递至输出层。在反向传播中,每个隐藏单元的参数梯度值相等。因此,这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代也是如此。在这种情况下,无论隐藏单元有多少,隐藏层本质上只有1个隐藏单元在发挥作用。因此,正如在前面的实验中所做的那样,我们通常将神经网络的模型参数,特别是权重参数,进行随机初始化。
PyTorch的默认随机初始化
随机初始化模型参数的方法有很多。在线性回归的简洁实现中,我们使用torch.nn.init.normal_()使模型net的权重参数采用正态分布的随机初始化方式。不过,PyTorch中nn.Module的模块参数都采取较为合理的初始化策略(不同类型的layer具体采样的哪一种初始化方法的可参考源代码),因此一般不用我们考虑。
Xavier随机初始化
(摘自课程讲解内容,个人对这部分理解并不是很清晰,有待继续读论文确认) 还有一种比较常用的随机初始化方法叫作Xavier随机初始化。 假设某全连接层的输入个数为 $a$,输出个数为 $b$,Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布 $$ U \left(-\sqrt\frac{6}{a+b},\sqrt\frac{6}{a+b}\right)$$ 它的设计主要考虑到,模型参数初始化后,每层输出的方差不该受该层输入个数影响,且每层梯度的方差也不该受该层输出个数影响。
五、考虑环境因素
协变量偏移
这里我们假设,虽然输入的分布$p(x)$可能随时间而改变,但是标记函数,即条件分布$p(y|x)$不会改变。虽然这个问题容易理解,但在实践中也容易忽视。
想想区分猫和狗的一个例子。我们的训练数据使用的是猫和狗的真实的照片,但是在测试时,我们被要求对猫和狗的卡通图片进行分类。
显然,这不太可能奏效。训练集由照片组成,而测试集只包含卡通。在一个看起来与测试集有着本质不同的数据集上进行训练,而不考虑如何适应新的情况,这是不是一个好主意。不幸的是,这是一个非常常见的陷阱。
统计学家称这种协变量变化是因为问题的根源在于特征分布的变化(即协变量的变化)。数学上,我们可以说$p(x)$改变了,但$p(y|x)$保持不变。尽管它的有用性并不局限于此,当我们认为x导致y时,协变量偏移通常是正确的假设。
标签偏移
当我们认为导致偏移的是标签$p(y)$上边缘分布的变化,但类条件分布是不变的$p(x|y)$时,就会出现相反的问题。当我们认为y导致x时,标签偏移是一个合理的假设。例如,通常我们希望根据其表现来预测诊断结果。在这种情况下,我们认为诊断引起的表现,即疾病引起的症状。有时标签偏移和协变量偏移假设可以同时成立。例如,当真正的标签函数是确定的和不变的,那么协变量偏移将始终保持,包括如果标签偏移也保持。有趣的是,当我们期望标签偏移和协变量偏移保持时,使用来自标签偏移假设的方法通常是有利的。这是因为这些方法倾向于操作看起来像标签的对象,这(在深度学习中)与处理看起来像输入的对象(在深度学习中)相比相对容易一些。
病因(要预测的诊断结果)导致 症状(观察到的结果)。
训练数据集,数据很少只包含流感 $p(y)$ 的样本。
而测试数据集有流感 $p(y)$ 和流感 $q(y)$,其中不变的是流感症状 $p(x|y)$。
概念偏移
另一个相关的问题出现在概念转换中,即标签本身的定义发生变化的情况。这听起来很奇怪,毕竟猫就是猫。的确,猫的定义可能不会改变,但我们能不能对软饮料也这么说呢?事实证明,如果我们周游美国,按地理位置转移数据来源,我们会发现,即使是如图所示的这个简单术语的定义也会发生相当大的概念转变。
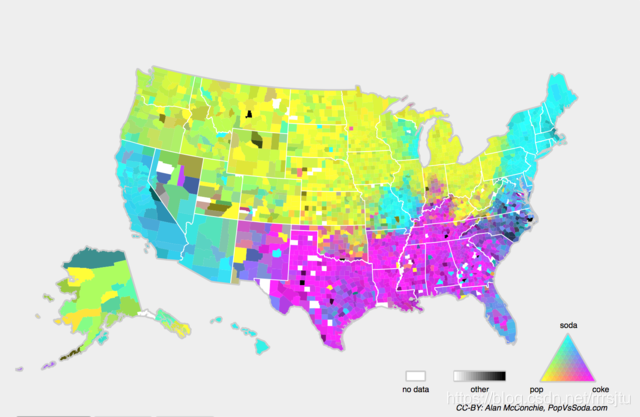
如果我们要建立一个机器翻译系统,分布 $p(y|x)$ 可能因我们的位置而异。这个问题很难发现。另一个可取之处是 $p(y|x)$ 通常只是逐渐变化。
Q&A
(摘自优秀答疑) 1. 训练集、验证集和测试集的比例应该怎么去进行分配呢? 答:传统上是6:2:2的比例,但是不同的情况下你的选择应当不同。这方面的研究也有很多,如果你想要知道我们在设置比例的时候应当参考那些东西,可以去看Isabelle Guyon的这篇论文:A scaling law for the validation-set training-set size ratio 。他的个人主页里也展示了他对于这个问题的研究。 2. 训练集、验证集和测试集的数据是否可以有所重合? 答:有些时候我们的数据太少了,又不想使用数据增强,那么训练集、验证集和测试集的数据是否可以有所重合呢?这方面的研究就更多了,各种交叉方法(例如之前提到的k-fold validation),感兴趣的话可以去看Filzmoser这一篇文章Repeated double cross validation